基于信息交互分析的建设工程变更预测

        引 言

        工程变更管理是建设项目实施过程管理中的一项重要内容。导致工程变更的原因很多, 如项目的复杂性、资源的有限性、工作和环境的不确定性、缺少及时有效的沟通等[1 2] 。要采取有效的措施减小变更对项目的不利影响就必须尽可能早地掌握变更事态[3] , 因此, 有学者提出了变更预测理论, 并应用于建设工程变更管理, 代表性的如Motawa和Anumba等应用模糊逻辑理论评估项目的稳定性( Projects stability) , 并在一定程度上实现了预测变更的目的[ 4] , 但上述变更预测方法并不能给出关于工程变更的详细信息。（参考《www.jianzhu518.com》）

        本文提出了基于工作的变更预测, 能够提供可能发生变更、变更量、变更所影响的工作等具体信息。通过项目实施过程中工作和工作之间、工作和非工作因素之间的信息交互分析, 应用基于工作的依赖结构矩阵( Dependency Structure Matrix, DSM )和依赖关系图分析法实现对变更发生过程的模拟, 从而实现在工作层次上对变更的预测。

        1 基于工作的依赖结构矩阵

        依赖结构矩阵( DSM ) 也称为设计结构矩阵( Design Structure Matrix ), 是一种以矩阵为框架表述信息流的方法, 适于分析多个工作之间的复杂信息交互关系[4] 。在建设项目管理领域, DSM 能用于表述:

        （1）可能的迭代和返工；（2）学习效应；(3) 随机的工作时间和成本；(4)资源约束；(5)搭接工作；(6)基于风险控制的并行返工管理；(7)过程模拟等[5] 。DSM 有四种不同类型: (1)基于成分的DSM；(2)基于团队的DSM；(3)基于工作的DSM；(4)基于参数的DSM。本研究使用基于工作的DSM 来模拟变更的发生过程, 从而实现对工程变更的预测。

        本文通过使用返工概率矩阵、返工工作量矩阵和工作逻辑关系矩阵来实现DSM 对变更发生过程的模拟。其中返工概率矩阵中的元素表示其所在行对应工作的改变导致其所在列对应工作发生返工的概率。上述变更如确实发生, 则元素对应列所代表的工作将发生返工, 返工工作量可以通过返工工作量矩阵进行计算。工作逻辑关系矩阵中的元素表示的是元素所在列对应工作和所在行对应工作之间的逻辑关系。

        基于工作的DSM 是一个n阶方阵, 行和列分别表示同一系列工作, 矩阵中元素代表各个工作之间的交互关系。矩阵中非对角线上的某个元素如果不等于0, 则表示元素所在列所代表工作和元素所在行所代表工作之间存在依赖关系, 并且前者的开始需要后者提供一定的信息才能进行[ 6] 。基于工作的DSM 矩阵具有表述工作之间复杂信息流的能力, 能用于表述建设项目工期和工作之间的关系, 可对复杂项目进行可视化分析。

        鉴于上述的返工概率为随机数据, 这就需要一种能够分析处理随机数据的过程模拟方法。由于蒙特卡洛模拟方法能够在已知系统内因素概率分布的情况下通过多次运算来模拟整个系统的概率分布, 本文将使用该方法实现对工程变更发生概率分布的计算。

        2 建设项目实施过程信息流建模

        2. 1 建设项目信息流

        建设项目的信息流主要有两类, 一类是工作和工作之间的信息流, 称为基于工作的信息流( Activity  Based Information Flow, AIF) ； 另一类是工作和非工作因素之间的信息流, 称为基于非工作的信息流( Non Activity based Information Flow, NAIF)。两类的区别在于信息流的源头不同, AIF的源头是工作, 而NAIF的源头是与工作间接相关的非工作因素, 如环境因素等。在建设项目实施过程中, 工作的改变可以认为是由于信息流的变化造成的。预测工程变更首先需要了解导致变更发生的原因以及变更发生的过程, 然后通过合适的过程模拟方法模拟这些原因和过程, 便能有效地预测变更的发生。本文考虑的导致变更的原因是工作与工作之间或工作与非工作因素之间信息流的变化造成的。通过使用能够表示这种信息交互关系的方法来模拟信息流变化对工作的影响。

        本文在建模过程中, 对信息流做了如下三点假设:

        （1）每个工作开始时或执行过程中都需要信息, 这种信息可以是由该工作的紧前或紧后工作提供, 或是由其他非工作因素提供, 也可以是由它们同时提供；

        （2）如果上述信息由于信息源的改变而发生了改变, 将会导致接收信息的工作发生改变；

        （3）工作结束时可以提供信息, 工作执行过程中也可以提供信息。

        2. 2 工作信息流建模

        基于工作的信息流是工程建设项目实施过程中最主要的交互关系。根据上述假设可将建设过程中的信息流分为三种, 分别为返工迭代信息流、搭接迭代信息流和循环迭代信息流。本文应用基于工作的DSM 表述上述三种信息流, 如图1。

       
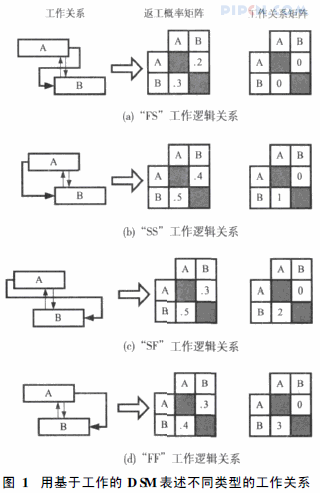
        图1 用基于工作的D SM表述不同类型的工作关系

        ( 1)返工迭代信息流( R ew ork Iteration InformationF low, R IIF)

        RIIF主要用于表示工作的变动, 该变动又是造成工程变更的主要原因。本文用基于工作的DSM 来表述RIIF, 其中矩阵DSMij1 和DSMij2分别表示返工概率矩阵和返工程度矩阵。DSM ij1中非对角线上的数值aij表示工作j的改变会有aij的概率导致工作i的改变, 这种概率也称为返工概率； DSM ij2中非对角线上的数值bij表示如果上述工作i改变了, 那么工作i的改变量为bij, bij以占工作i总工作量的百分比表示, 称为返工百分比。

        ( 2)搭接迭代信息流( Overlapping Iteration InformationFlow, OIIF)

        假设两个相互依赖的工作按顺序搭接施工, 紧后工作的开始需要紧前工作完成后提供的信息才能继续实施, 但由于工作搭接, 紧后工作的开始时间要早于紧前工作的完成时间, 因此, 就要在紧后工作开始时对其所需要的紧前工作的信息做出假设。当紧前工作完成后, 如果提供给紧后工作的信息不同于开始时紧后工作对紧前工作信息的假设, 则就需要对紧后工作中的部分或全部工作进行返工。而且由于紧后工作开始时间的提前, 也可能导致紧前工作做相应的改变。

        搭接是压缩项目建设时间最常采用的方法之一, 但使用搭接技术往往需要更多的费用和更复杂的管理[ 7] 。本文在OIFF建模过程中引入工作关系矩阵表示工作之间的搭接关系, 如图1所示: 工作关系矩阵中的“0”表示工作A 和B 之间是结束到开始的工作逻辑关系( FS)；“1”表示工作A 和B之间是“开始到开始”的工作逻辑关系(SS)； “2”表示“开始到结束”的工作逻辑关系( SF)；“3”表示∋结束到结束(的工作逻辑关系( FF)。

        ( 3)循环迭代信息流( Sequential Iterations Information Flow, SIIF)

        如图1中( c)的返工概率矩阵即是一个标准的返工环路: 工作A的开始是基于对工作B 信息的假设,当工作B 开始后会对工作A输出新的信息(即更新工作A 对工作B 信息的假设), 新信息的输入可能会导致工作A 返工。由于工作B 的返工而导致工作A 再次变更的现象称为二次返工。实际工作中, 二次返工所需的时间往往比一次返工要少得多, 这是由于再次做同样的工作所需时间要比第一次做所需的时间少,这种现象被称为∋学习效应(, 可以用返工影响矩阵结合学习曲线来表示此类情况[ 8] , 如式( 1)。

        调整后的返工工作量= 工作x 的返工工作量)×(学习率)^阶数 (1)

        2. 3 非工作信息流建模

        与环境、政府和项目员工等相关的因素是典型的可能导致变更发生的非工作因素。类似于工作信息流, 对非工作信息流的处理也可以转换为非工作因素和工作之间的返工影响关系。但由于许多非工作因素都不是直接影响工作的, 这就需要使用某些方法将这种间接的影响转换为可以使用返工量来表示的直接影响, 本文以依赖关系图为工具定量分析非工作信息流对工作的影响, 如图2示例。



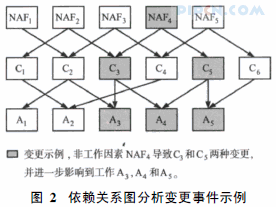
        图2 依赖关系图分析变更事件示例

        2. 4 扩展依赖结构矩阵的构建

        模拟建设项目实施过程通过以下四步实现:( 1)获得项目的工期计划数据, 一般可从CPM 或GERT中得到；

        ( 2)分析计划工作之间的基于工作的信息流, 并用基于工作的DSM 的形式和返工概率、返工工作量来表述；

        ( 3)用依赖关系图分析建设项目实施过程中非工作因素和工作之间的信息流, 也用DSM表述；

        ( 4)综合上述分析结果, 构建基于工作的扩展矩阵, 如图3。