文本分类中词语权重计算的改进

        1概述

        随着各种电子形式的文本文档如电子出版物、各种电子文档、电子邮件和万维网等文本数据库等以指数级的速度增长，有效的信息检索、内容管理以及信息过滤等应用也变得越来越重要。文本的自动分类是有效的解决办法之一，并且已经成为一项具实用价值的关键技术。而文本分类所要解决的首要问题就是文本的形式化表示[1]。（参考《www.jianzhu518.com》）

        在现有的几种文本表示模型中，向量空间模型（VSM）由于具有较强的可计算性和可操作性，得到了广泛了应用并且取得了较好的效果。在该模型中，文档的内容被形式化为多维空间中的一个点，通过向量（vector）的形式给出[2]。因此，向量空间模型文本表示的形式化方法是基于文本处理的各种应用得以实现的基础和前提。基于此，本文针对向量空间模型中经典的词语权重计算方法的不足之处提出了一种结合信息论中信息增益的改进算法，并通过验证了其可行性和有效性。

        2传统的TFIDF

        传统的特征权重计算主要考虑特征项的频率信息TF以及反文档频率信息IDF[3]。

        2.1特征项频率（Term Frequency,TF）

        TF是特征项频率，它是指特征项在文档中出现的次数。特征项可以是字、词、短语，也可以是经过语义概念词典进行语义归并或概念词语权重计算方法后的语义单元。不同类别的文档，在某些特征项的出现频率上有很大差异，因此频率信息是文本分类的重要参考之一。它的计算公式为：

       

        2.2反文档频率（Inverse Document Frequency,IDF）

        IDF以出现特征词的文本数为参数来构建特征项的权重。其计算方法的出发点是一个特征词文档频数越高，那么其包含的类别信息就越低，也就表示该特征词就越不重要。IDF的计算公式为：

       

        其中N为文档集的总文档数，ni为出现特征项ti的文档数。计算对数时，由于我们计算的权重值是相对的，所以底数可为任意实数，这里用2作为底数计算。

        一个有效的分类特征项应该既能体现所属类别的内容，又能将该类别同其它类别区分开来。所以，在实际应用中通常将TF与IDF联合起来使用。公式如下：

       

        由于各类别文本的长度很难一致，各类文本包含的字数、词数可能差别会很大，对词频造成直接影响，因此通常对词频作归一化处理。TFIDF的归一化计算公式如下：

       

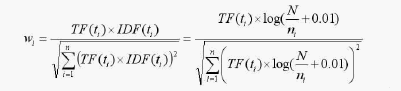
        其中wi为第i个特征项在文本中的权重，TF（ti）是特征项ti在文本dj中出现的频数，n表示特征向量的维数。

        3传统TFIDF权重计算方法分析

        TF.IDF权重计算方法主要从词语的频率TF和词语的反文档频率IDF两个方面进行考虑。计算公式的提出是基于这一假设：对区别文档类别最有意义的词语是在一个文档集合中出现频率足够高，并且在其它文档集合中出现频率足够少的词语。所以，向量空间模型的基础是词语的出现频率和出现文档频率。

        这种方法中IDF值的计算是将训练文本集看作一个整体来考虑的，并没有考虑到特征项在类间的分布信息。比如说：如果某一类ci中包含特征项t的文档数为m，而其他类包含t的文档总数为k，显然所有包含t的文档数n=m+k，当m大时，n也大，根据公式可以得到，IDF的值就越小，则根据TFIDF的计算方法，权重值也会受到影响。但实际上，m大的话，表示t在ci类的文档中频繁出现，就说明t能够很好地代表ci类的文本特征，应该赋予较高的权重。

        可以通过一个很小的文档集来说明权重计算方法TFIDF的利弊问题，假设有三个类别c1，c2，c3，每个类别中都各有5篇文档，为了计算方便这里只考虑三个特征项t1，t2，t3。

       

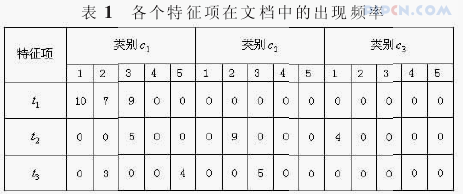
        从表1可以看出：t1只有类别c1中出现，所以其分类能力应是最强的；而t2在三个类别中均出现了，所以其分类能力应是最弱的。但是我们来看看他们的IDF的计算结果。如表2所示。

       

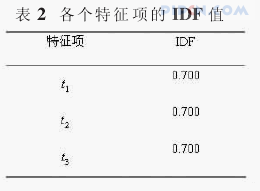
        从表中我们可以看到，t1、t2、t3三个特征项的IDF值是相同的，那么其权重大小就完全取决于TF的值，也就是特征项在每个类别中出现的次数，而这显然是很不合理的。出现这种情况的原因，主要是因为计算IDF是基于训练集合中所有文档来考虑的，没有区分特征项在不同类别中的出现的文档数，当然也就无法表示出特征项和类别间的关联性。

        为了弥补这一不足，在计算权重时，引入信息增益的概念。

        4信息增益（information gain,IG）的引入

        4.1信息熵和信息增益

        1850年，德国物理学家鲁道夫·克劳修斯首次提出“熵”的概念，用来表示任何一种能量在空间中分布的均匀程度，能量分布得越均匀，熵就越大[4]。1948年，信息论之父C.E.Shannon提出了“信息熵”的概念，解决了对信息的量化度量问题，并且第一次用数学语言阐明了概率与信息冗余度的关系[5]。

        信息熵，又称Shannon熵，在随机事件发生以前，它表示结果不确定性的量度；在随机事件发生以后，它表示我们从事件中所得到的信息的量度（信息量）[6]。

        信息论量度信息，是把获得的信息看作用来消除不确定性的东西，信息量的大小用被消除的不确定性的多少来表示。假设随机事情X在获得信息y之前的不确定性为H(X)，获得信息y之后为H(X/y)，信息y中包含的关于事件X的信息量为：

       

        假如信息概率空间为，那么其不确定度可以表示为：

       

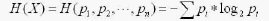
        条件熵是H(X/y)获得信息y后X的不确定程度。

        信息增益是信息熵的差，表示为：

       

        H(X)表示在获得信息y之前系统的熵。对于文本分类而言，其表示的是一个随机文档落入某个类的概率空间的熵，即类别集合X所能提供的信息量的多少。H(X/y)表示获得y后，此文档落入某个类的概率空间的熵，即观察到y之后所能提供的信息量。这种不确定程度减少的量也就是信息增益，代表y对分类所起到的作用，即它所能提供的分类信息量。

        4.2用信息增益来调整权重

        我们从信息论的角度出来，把信息增益考虑进了词语在各文档中的分布比例对权重的影响中。将训练文档集看成一个符合某种概率分布的信息源，词语在文本分类中所能提供的信息量（也就是词语在分类中的重要程度）依靠训练文档集的类别信息熵和文档类别中该词语的条件熵之间信息量的增益来确定。并且将这种重要程度反映到了权重计算公式中，提出了如下TF.IDF.IG权重计算公式：

[1] [2]  下一页