盾构施工对地表沉降影响的预估
摘 要: 以杭州地铁 1 号线过江隧道为背景, 采用经验公式法和有限元数值模拟方法研究分析盾构隧道施工引起的钱塘江北岸标准海塘地表沉降规律, 比较两种方法的计算结果, 验证了有限元数值模型的合理性, 为隧道工程的顺利实施提供参考依据。(参考《www.jianzhu518.com》)
关键词: 盾构隧道; 数值模拟; 地层变形
杭州地铁 1 号线南起萧山湘湖杭州乐园, 穿过滨江新中心, 至钱塘江时在最低冲刷高程以下通过江底, 直达江北岸进入婺江路下, 并沿该路西行。过江隧道采用加泥式土压平衡盾构施工,采用钢筋混凝土管片单层装配式衬砌。盾构隧道外径 6.2 m, 内径 5.5 m, 衬砌厚度 35 cm, 环宽1.2 m, 衬砌环全环由 6 块组成, 环与环、块与块间均采用弯螺栓连接。
过江隧道盾构掘进时不可避免地引起地层扰动, 引起地层变形及地面沉降。扰动导致土体强度和压缩模量的降低, 这将引起长时间的固结和次固结。当地层变形超过一定范围时, 会严重危及周围建筑物的安全。因此, 掌握地层沉降规律并预先评估其影响程度, 对工程的顺利实施极为重要。本文采用经验公式法和有限元数值模拟方法对钱江通道盾构隧道施工过程中明清鱼鳞石塘的地表沉降规律进行研究, 以期对海塘的保护措施及隧道工程的顺利实施提供参考依据。
1 盾构隧道引起土层变形的发展过程盾构推进引起的地面沉降分为 5 个阶段[1-2]:
1) 初期沉降: 即盾构开挖面到达某一位置之前, 在盾构推进前方的土体滑裂面以外产生的沉降。因初期沉降量较小, 所以一般不被人们觉察。
2) 盾构到达时的地面变形: 为在开挖面靠近观测点并到达观测点下方过程中所产生的沉降或隆起现象。当盾构机的正面土压力等于开挖面静止土压力时, 掘进对土体影响最小; 当盾构机推力不足, 其正面土压力小于开挖面的静止土压力时, 开挖面土体下沉; 当盾构机推力过大则会引起开挖面土体的隆起。
3) 盾构通过时的地面变形: 为盾构机开挖面到达观测点至盾构机尾部通过观测点这一过程所产生的沉降。该沉降主要是由于盾构机的通过破坏了原来的土体状况, 造成土体的扰动所致。
4) 盾尾空隙沉降: 由于盾尾通过时会产生一个盾尾间隙, 这个盾尾间隙的上方及周围土体应力释放引发了弹塑性变形。
5) 长期延续沉降: 由于盾构通过时对地基土产生了扰动, 再加上上面的各种残余影响, 在相当长的一段时间内, 地基将继续发生固结沉降和蠕变沉降。
2 地层隆沉估算
2.1 地面沉降横向分布计算
地表沉降横向分布曲线的形状可用 Peck[3]公式合理地表达, 这一概念已被人们所接受, 上海地区的许多盾构施工实例也充分证明了它的实际使用效果[4-5]。Peck 假定施工引起的地面沉降是在不排水情况下发生的, 沉降槽的体积等于地层损失的体积。地层损失在隧道长度上是均匀分布的,隧道施工产生的地表沉降横向分布近似为一正态分布曲线:
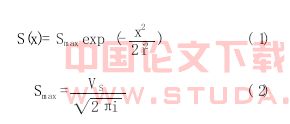
式中: S (x)为距离隧道中心线处的地表沉降 ( m) ;Smax 为隧道中心线处最大地面沉降 ( m) ; x 为距隧道中心线的距离 ( m) ; i 为沉降槽宽度系数 ( m) ;VS 为盾构隧道单位长度地层损失 ( m3/m) 。
Peck 公式中的 VS ( 地层损失) 与盾构种类、操作方法、地层条件、地面环境、施工管理等因素有关, 目前尚难给出确定的解析式。根据统计,在采用适当技术和良好操作的正常施工条件下,地层损失 VS 可表示为:
VS=VlπR2 ( 3)
式中: Vl 为地层体积损失率, 即单位长度地层损失占单位长度盾构体积的百分比; R 为盾构机外径 ( m) 。
沉降槽宽度系数 i 决定了盾构施工对周围土体的影响范围, 一般而言, 沉降槽半宽为 2.5i。研究表明, i 取决于接近地表的地层的强度、隧道埋深和隧道半径, 其计算式如下:
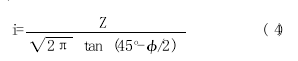
式中: Z 为地面至隧道中心的深度; Ф为土的内摩擦角。
杭州地铁 1 号线过江隧道外径为 6.2 m, 土内摩擦角取为 23.2°, 隧道顶部覆土厚度有 18.8 m,运用 Peck 公式计算可得沉降槽半宽 W/2=33.0 m,计算结果见表 1, 地面沉降横向分布见图 1。
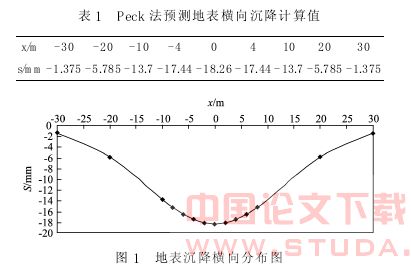
2.2 地面沉降纵向分布计算
刘建航[6]院士在 Peck 法的基础上, 提出了负地层损失概念, 并将地层损失分成开挖面和盾尾后的地层损失两部分, 得出了地面沉降量的纵向分布预测公式:

式中: S(y)为距原点距离 y 的地面沉降量, 负值为隆起量, 正值为沉降量 ( m) ; Vl1为盾构开挖面引起的地层损失, 欠挖时为负值 ( m3/m) ; Vl2为盾构开挖后, 以盾尾空隙压浆不足及盾构改变推进方向为主的所有施工因素引起的地层损失 ( m3/m) ;
y 为沉降点至坐标原点的距离 ( m) ; yi 为盾构推进点处盾构开挖面至坐标原点的距离, yf 为盾构开挖面至坐标原点距离 ( m) :
yi′=yi- L; yf′=yf - L
L 为盾构长度 ( m) ; Φ( y) 为正态分布函数的积分形式。
纵向沉降槽宽度系数 iy 和横向沉降槽宽度系数 ix 可通过修正系数 K 联系起来:
iy= Kix ( 6)
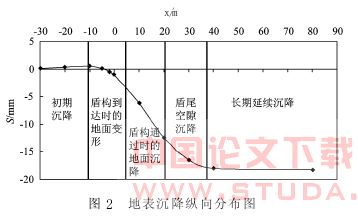
随着盾构隧道的推进, 鱼鳞石塘地表沉降发展过程如图 2 所示。
由图 2 可知, 盾尾空隙沉降和长期延续沉降占总沉降的比例为 50%~80%。
3 有限元分析法预测地层沉降
随着有限元法和计算技术的发展, 数值模拟法在预测分析盾构隧道引起的地层变形中被广泛应用。钱江通道过江隧道采用双管单层双向六车道盾构方案, 传统的经验方法无法很好地完成地层变形评估, 而有限单元法不仅可以模拟双线隧道, 而且可以考虑地层结构, 适应复杂边界条件,提供更为丰富全面的计算成果, 更适合地层变形分析。本文采用荷兰 Delft Technical University 研制的有限元分析软件 PLAXIS 模拟隧道施工导致的地面沉降, PLAXIS 是一个专门用于岩土工程变形和稳定性分析的有限元计算程序。
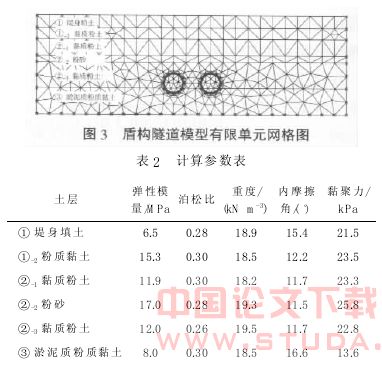
该模型考虑的隧道直径为 6.2 m, 隧道中心埋设高程为-11.92 m, 盾构隧道顶部覆土厚度为 18.7m,两隧道间距 6.0 m, 影响区域土体 100 m×40 m。地基土层包括 6 个不同土层, 由上而下分别是堤身填土, 厚 4.0 m; 黏质粉土, 厚3.5 m; 黏质粉土, 厚 5.4 m; 粉砂, 厚 2.1 m; 黏质粉土, 厚 8.3 m;淤泥质粉质黏土, 厚 8.5m; 更深部分则被看作完全坚硬, 以合适的边界条件加以模拟。土孔隙水压力分布是静态水压, 水位高程 ( 参考地质勘察报告) 取为 6.5 m。数学模型如图 3 所示。土层采用 MOHR- COULOMB 模型, 隧道衬砌采用线弹性, 厚度为 0.35 m。数模分析中考虑的荷载有结构自重、水土压力, 模型采用 15 节点单元为基本单元类型, 共有 582 个单元, 4 901 个节点。计算参数见表 2。
3.2 数模计算分析
3.2.1 第 1 条隧道开挖后的地表沉降
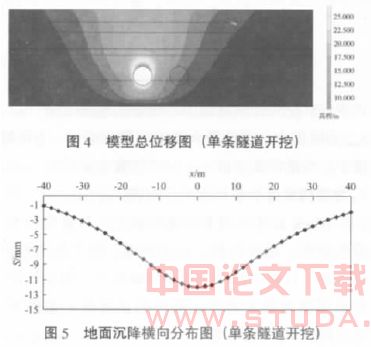
数值模拟计算结果见图 4, 图 5。图 4 表明单条隧道开挖后, 造成了地表下陷, 土层沉降对称分布, 最大沉降出现在施工隧道中心轴线处, 隧道上方的地层沉降随深度增加而增加, 在接近隧道衬砌顶端位置达到最大, 在隧道下方土体出现向上的位移, 在隧道衬砌底端达到最大。由图 5可知地表最大沉降为 12.00 mm。
3.2.2 二条隧道都开挖后的地表沉降
数值模拟计算结果见图 6, 图 7。计算结果显示, 隧道轴线正上方地表沉降最大, 向左右沉降分别逐渐减小, 由于新老隧道开挖的相互影响,地表最大沉降为 22.22 mm, 比经验公式计算结果大 3.96 mm。
