竖井联系测量在地铁建设中的应用
摘 要 以广州地铁的控制测量为例,介绍地铁施工中竖井联系测量的3种方法:陀螺定向法、钻孔投点法和联系三角形法。(参考《www.jianzhu518.com》)
关键词 竖井联系测量 陀螺定向法 钻孔投点法 联系三角形法
城市地铁建设主要是通过竖井提供工作面进行施工,如何保证井下按设计开挖就成为施工的首要问题。竖井联系测量(平面)的目的就是将地面控制网的坐标和方位按要求精度准确地传递给井下导线,为施工提供依据。笔者根据参加广州地铁控制测量的工作经验,将广州地铁竖井联系测量所采用的几种方法总结如下,供地铁测量工作参考应用。
1 陀螺定向法
陀螺定向法是采用光学垂准仪(或重锤球)投出井上、井下在同一铅锤线上的点位,根据井上、井下陀螺定向成果,求算投点在空间的平面夹角,使得井上、井下的导线连成一体,把井上导线坐标、方位传递到井下导线。
下面以广州地铁杨体区间竖井联系测量为例,介绍陀螺定向法实施的特点。
1.1 仪器设备
TC1610全站仪,GAK1 T2陀螺经纬仪,NL光学垂准仪。
1.2 作业实施
(1)竖井投点
井上、井下导线布置情况如图1所示,供电局、J54、A为井上已知导线点,Z1、Z2、Z3为井下待求导线点。在井口选定T1、T2两个点位,在井盖上相应位置预留有可遮盖的小孔,将垂准仪置于小孔上方,垂准仪在井上及井下投下T1和T1′、T2和T2′。T1、T1′在空间上为2个点,但投影到同一平面时就成为1个点;T2、T2′情况相同。井上、井下导线通过投点连成一闭合环。
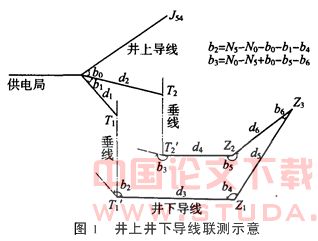
(2)陀螺经纬仪定向
定向时采用逆转点法进行。对一条边定向时,完成一端定向为半测回,完成两端定向为一测回。由于井筒上下不宜安置陀螺经纬仪,故井上选择AJ54为定向边,井下选择Z1Z3为定向边,进行陀螺定向观测。求出陀螺仪的定向常数,并进行改正。
假定陀螺经纬仪测得的AJ54陀螺方位角为N0,Z1Z3陀螺方位角为N5。
(3)导线边角测量
①测b0、b1、b4、b5、b6角度;
②量d1、d2、d3、d4、d5、d6边长。
(4)空间夹角计算b2为AT1、T1′Z1在空间上的夹角,b3为AT2、T2′Z2在空间上的夹角。
(5)导线计算
根据以上导线测量成果,进行导线平差计算。坐标、方位从井上导线点传递到井下导线点,Z1、Z2、Z3坐标成果用于指导施工。
1.3工作体会
①陀螺定向法的主要优点是占用井筒时间短、精度高、观测作业简单,在地铁施工的竖井中均可采用此方法进行联系测量,是一种值得推广应用的作业方法。
②陀螺定向的实质是通过投点、定向,把井上、井下的导线联成一体,陀螺经纬仪起了测空间边夹角的作用。
③陀螺定向应选择固定边进行,每条边由不同的观测员观测1~2个测回。以后再进行竖井联系测量时,陀螺定位应在上次定位边上进行,以利检核。
④陀螺定向法的不足之处是陀螺经纬仪的价格昂贵,拥有陀螺经纬仪的单位较少,难以推广应用。
2 钻孔投点法
钻孔投点法是根据地铁浅埋的特点,应用一根垂线上平面坐标相同的原理而总结出的竖井联系测量方法。下面以广州地铁东杨区间2号竖井为例,对钻孔投点法作一介绍(如图2所示)。
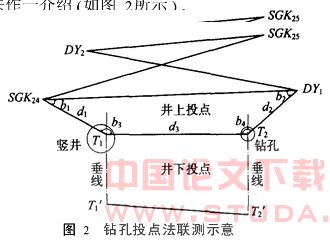
2.1 仪器设备
东杨区间按钻孔投点法进行联系测量时,使用的仪器设备为TC1610全站仪和NL垂准仪,并聘请有钻机的单位予以配合。
2.2 作业实施
(1)导线布设
根据现场情况,选择竖井井盖上一点为T1(利用竖井,不需钻孔);在已经开挖的竖井通道或中线导洞上方选择一点T2,并用钻机钻出约20cm的圆孔。地面投点T1、T2,从地面已知导线SGK24、SGK25、DY 2、DY1引测。
(2)钻孔和竖井投点
钻孔投点与竖井投点的方法及要求相同:利用垂准仪在竖井和钻孔分别投出井上点T1、T2和井下点T1′、T2′。地下投点T1′、T2′要预先埋设固定钢标,投点后刻好标记。
(3)地面投点坐标
地面投点T1、T2边角测量:测b1、b2、b3、b4角度,量d1、d2、d3边长。
根据以上测量成果,计算出T1、T2坐标。
如前所述,因地下投点T1′、T2′和地面投点T1、T2分别位于同一根垂线上,所以取T1′坐标等于T1坐标,T2′坐标等于T2坐标。T1′、T2′用于指导洞内施工。
2.3工作体会
①钻孔投点法是一种适合于浅埋(埋深小于30m)工程的竖井联系测量方法,具有作业时间短、测量精度高、简单直观、容易操作的特点。当具有钻孔条件时,地铁竖井应优先考虑采用此法进行联系测量。
②当工程埋深大于30m时,应结合钻孔费用、投点误差、投点作业环境等具体情况,慎重考虑是否采用钻孔投点法。
③钻孔投点距离以大于150m为宜,以减少投点误差对坐标方位的影响。
④钻孔投点法不足之处是准备工作繁多,如恢复地面中线,确定投点位置;寻找钻孔队伍,现场钻孔等;不利于钻孔投点法的推广应用。
3 联系三角形法
联系三角形法是一种传统的竖井联系测量方法。下面以黄沙盾构竖井联系测量为例对联系三角形法作一介绍(如图3所示)。
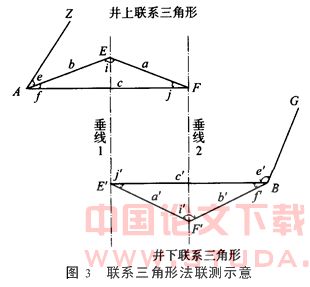
3.1 仪器设备
TC1800全站仪;10kg重锤2个;Φ0.5mm高强钢丝60m;小绞车、导向滑轮及经过比长的钢卷尺等。
3.2 作业实施
(1)导线布设
导线布设情况如图3。垂线1、垂线2是通过竖井绞车及导向滑轮悬挂并吊有垂锤的高强钢丝。Z、A为已知的地面导线点,B、G为待求的井下导线点,井下、井上三角形布设时应满足下列要求:
① 垂线边距a、a′应尽量布置长些;
② e、f、e′、f′角度应尽量小,最大不应大于2°;
③b/a、b′/a′'之比值应尽量小,最大值不应大于1 5。
(2)三角形测量
①测e、f、e′、f′角度;
②量a、b、c、a′、b′、c′边长。
(3)三角形平差计算
根据a、b、c、f求j:sinj=bsinf/a
c的计算值:c算=bcosf asinj
c的不符值:h=c算-c
a边改正值:Δa=-h/4
b边改正值:Δb=-h/4
c边改正值:Δc=h/2
以改正后的边长a、b、c为平差值,按正弦定理计算出i、j,即为平差后的角值。f改正很小,仍采用原测角值。
采用上述方法可计算出井下三角形平差后的边角a′、b′、c′、i′、j′。f′改正很小,仍采用原测角值。
(4)坐标和方位传递计算
已知A点坐标为XA、YA,AZ方位角为Z0。根据平差后的三角形边角进行计算。
① BG方位角Z0′
AF方位角Z1=Z0 e
FE方位角Z2=Z1 180 j
E′B方位角Z3=Z2 180-j′
求算边BG方位角Z0′=Z3 180 e′
②B点坐标
XB=XA ccosZ1 acosZ2 c′cosZ3
YB=YA csinZ1 asinZ2 c′sinZ3
(5)重复观测
进行联系三角形测量时,为保证精度,要重复观测数组。每组只将两垂线位置稍加移动,测量方法完全相同。由各组推算井下同一导线点之坐标和同一导线边之坐标方位角。各组数值互差满足限差规定时,取各组的平均值作为该次测量的最后成果。
3.3工作体会
联系三角形法是一种传统的竖井几何联系测量方法,存在设备笨重、工序繁多、工作时间长、劳动强度大等不足,与其他方法相比已显得比较落后。只是在不具备其他方法作业条件的情况下,可采用此法进行竖井联系测量。
参考文献
[1] TB10101—99 新建铁路工程测量规范[S]
[2] GB50308—1999 地下铁道、轻轨交通工程测量规范[S]
[3] GB50026—93 工程测量规范[S]
