壁挂式空调制冷与制热运行的数值模拟
摘要:利用湍流κ-ε、κ-ω方程计算了壁挂式空调的制冷与制热运行时的三维速度与温度场,分别比较了制冷与制热运行时3个不同坐标平面内的速度与温度分布,为分析空调的设计运行参数提供依据。
关键词:空调器 CFD 流场 温度场
1引言
空调设计是以经济技术合理的系统以及设备选型实现所要求的室内气候环境(温度、气流、污染物浓度等的分布).为实现对这些环境参数的合理控制,有必要把握其分布特征,CFD计算是除模型实验以外的可详细研究室内气流分布特征的重要手段〔1-41.相比传统的模型实验与经验公式预测流体的流动与传热,CFD计算具有成本低、速度快、资料完备等优点.
很多学者对空调的气流组织进行了深入的研究,这些研究大多采用稳态的模型,其研究大多不考虑室内与室外的热源、房间内部主要是空态的,这与实际运行时的情况有一定的区别.本文的研究是比较壁挂式空调在窗辐射、室内热源与墙体热源的情况下,对室内三维流场、速度场进行计算模拟,分析室内的流场与温度场.
2 几何模型
为了简化实际问题,便于分析,在建立数学模型前对室内气体的流动作如下假设:
1)室内气体满足牛顿内摩擦定律,为牛顿流体;2)室内气体温度变化不大,密度可视为常数;3)室内气体的流动形式为稳态紊流;4)在紊流中心区,忽略能量方程中由于粘性作用而引起的能量耗散.
以传统室内壁挂式空调为研究对象,对其温度场进行数值模拟计算.
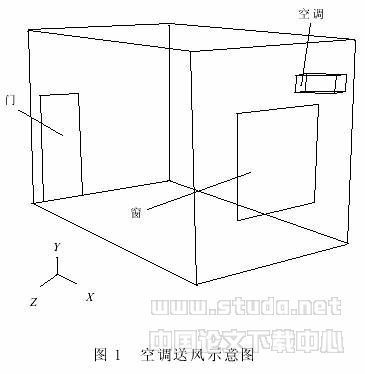
建立房间三维立体模型,长、宽、高分别为 5 m、4 m、3 m. 如图 1,空调安装高度为 2.5 m. X、Y、Z 3 方向坐标也表示于图中,设定空调的原始参数如下.
几何尺寸:800 mm×300 mm×200 mm;出风角度:45°;
出风速度:送风速度 2.6 m/s;制冷量:2500 W;
出风温度:制冷时 18℃,制热时 18℃.
根据已知参数,建立适当的房间有限元模型.为使结果尽可能接近真实情况,边界条件设定为:6 面墙处于绝热状态,制冷运行时的壁面固定温度为 30℃(制热时为 5℃),空调本身不发热,房间内部无任何热源.
2.1 k -ε 方程模型
数学模型采用 k -ε 双方程模型[3]. 模型的基本微分方程包括连续方程、动量方程、紊动能 k方程及紊动能耗散率ε方程,分别表示如下:
k 方程: 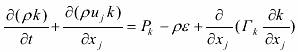
ε 方程: 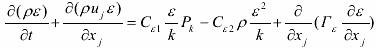
式中: 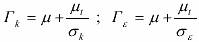
ρ 和 μ 分别为容积分数平均密度和分子粘性系数; μt 为紊流粘性系数,它可由紊动能 k 和紊动能耗散率 ε 求出:
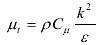
式中,Cμ =0.09 为经验常数. σk 和 σε 分别为 k 和 ε 的紊流普朗特数,其中 σk =1.0,σε =1.3. Cε1=1.44 和 Cε2 =1.92 为 ε 方程常数. Pk 为由平均速度梯度引起的紊动能产生项,定义为:
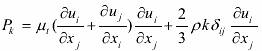
数值求解算法采用控制容积法,在每个控制容积单元中对微分方程进行积分,再将积分方程线性化,把控制方程离散为可以数值求解的代数方程,就可以得到相应各未知变量,如压力、速度、紊动能 k 及其耗散率 ε 等变量的代数方程组,然后再对方程组进行求解,就可以求出各未知变量及其空气的温度(或焓值和).
2.2 k -ω 方程模型
k 方程:
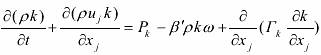
ω 方程:
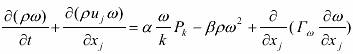
式中:
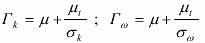
ρ 和 μ 以及 μt 的意义同 k -ε 方程的说明;
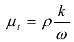
式中的几个主要常数的值如下: β′=0.09, σk =2.0, σω =2.0, α =5/9, β =3/40 .
3 模拟结果与分析
有了以上的数学模型和物理边界条件,笔者模拟了该空调房间的流场和温度场,并选取了其中具有代表性的断面进行分析,模拟结果见以下各图(图 2~7).
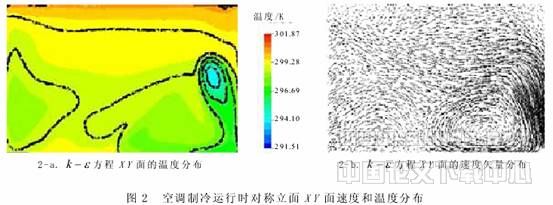
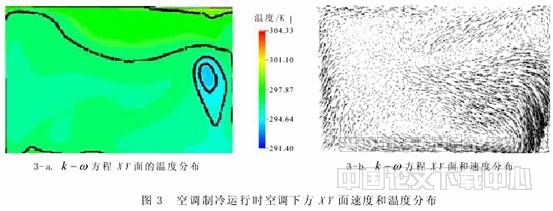
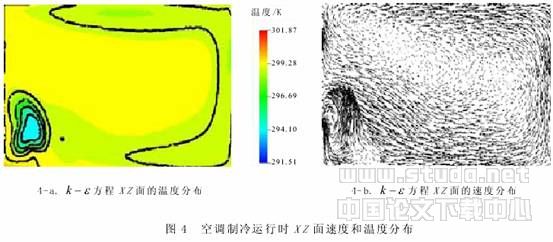
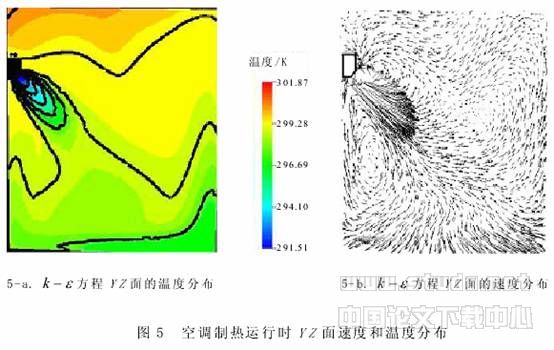
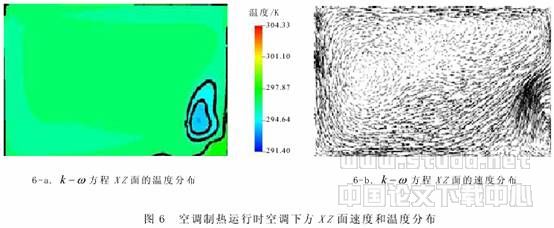
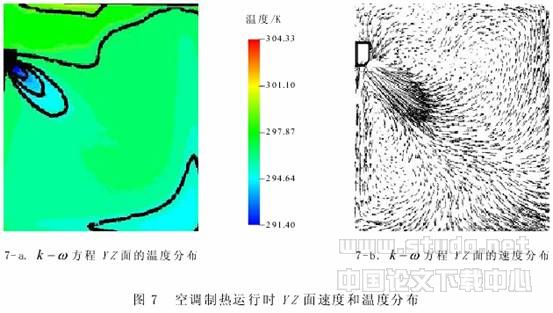
由上述空调的两种运行状况可以看出:在空调制冷运行时,由于冷空气自身的下坠,靠近地面的水平面的温度较低;由于空调射流的自身卷吸作用,加速了冷热空气的混合,从而使其室内温度场分布较为均匀. 在空调制热运行时,由于热空气的浮力作用,热空气难以到达地面附近,在人体垂直方向上存在温度梯度,头部比脚部温度高,这是由于冷空气较热空气密度大,向下趋势明显,从而导致房间下部要比上部降温快. 温度差会造成人体局部性热感不适,随着时间推移温度梯度会逐步渐小.
4 结论
本文利用湍流 k -ε 、 k -ω 方程计算了壁挂式空调的制冷与制热运行时的三维速度与温度场,分别比较了制冷与制热运行时 3 个不同坐标平面内的速度与温度分布. 空调的制冷与制热运行的两个工况,制冷运行中出现了冷风下坠现象,在制热运行中有部分热空气未经充分热交换而直接回流,能量利用不充分,温度均匀性也不好. 利用 CFD 计算可以改善室内的气流组织,通过改变空调不同气流出口速度、不同的出口角度从而得到合理的气流组织形式,这是采用传统的射流理论无法做到的.
