乳化沥青改性水泥砂浆的细观结构数值研究
摘要:文章建立了一个用于计算乳化沥青包裹水泥颗粒的计算模型,并根据试验测得的材料参数,利用复合材料有效弹性模量计算方法,对乳化沥青改性水泥砂浆的弹性模量进行数值分析。
关键词:乳化沥青;水泥砂浆;弹性模量
现在随着土木工程的不断发展,对于水泥砂浆的性能提出了更多方面的要求。在对混凝土静态力学性能的研究中,除了可以利用已被广泛采用的随机骨料模型、格构模型等细观力学模型分析混凝土的力学性能以外,以细观力学的观点建立其他模型用于分析水泥砂浆的力学性能。本文将在试验基础上,利用细观力学模型对乳化沥青改性水泥砂浆的弹性模量进行分析。
利用细观力学理论研究有效模量的常见方法有弹性力学解法、材料力学的半经验解法、随机统计法、自恰理论和广义自恰理论、微分法、相关函数积分法和平均场法。以上各方法虽然建立起了复合材料的细观量与宏观量的关系,但不能给出局部场的细节。20世纪70年代出现了均匀化理论用于分析两个或更多个长度尺度的物理系统。80年代该理论得到进一步发展。均匀化理论是一套严格的数学理论。该方法用均质的宏观结构和非均质的具有周期性分布的细观结构描述原结构。一点的细观结构认为是具有细观尺度的代表单元在空间上重复堆积而成,通过同时引入宏观尺度和细观尺度,可以详细地考虑材料细观结构的影响。由于均匀化理论的严密性、有效性,本文将采用该方法进行材料的有效性能计算。
一、细观力学模型
本文研究的对象为乳化沥青改性水泥砂浆,在细观层次上被视为一种三相复合材料。乳化沥青改性水泥砂浆中,由于有乳化沥青的存在,使部分未水化的水泥颗粒被乳化沥青包裹,形成类似于球状的结构,并填充于水泥水化产物形成的间断的、孔隙较大的网状体系中。整个水泥砂浆之中的包裹了未水化水泥颗粒的乳化沥青的分布情况,可以是随机的,也可以是均匀的。但是,从宏观上来看,它是均匀的,故只选取一个代表单元,就可以代表整体。又由于代表单元的尺寸远小于整体尺寸,因此可将它看作一个物理点。对于宏观均匀的复合材料,任意取一个或者几个代表单元进行研究,其结果都是一样的。
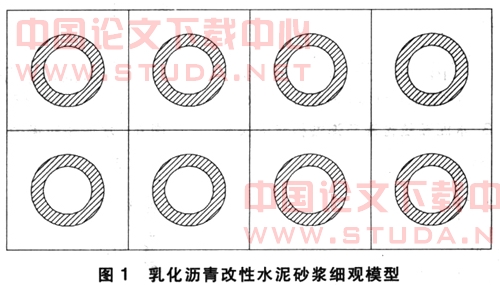
在本文中,只对乳化沥青改性水泥砂浆在二维平面的情况进行分析,同时作以下假设:第一,在乳化沥青改性水泥砂浆中,包裹了乳化沥青的未水化水泥颗粒半径是相同的,分布是均匀的,而且是各向同性的;第二,在乳化沥青改性水泥砂浆中,除了包裹了乳化沥青的未水化水泥颗粒以外其他未充分水化的水泥颗粒均被视为已完全水化,即作为砂浆相考虑;第三,细观力学模型中只考虑三相材料——未水化水泥颗粒、乳化沥青和水泥砂浆,不考虑孔隙及杂质等成分;第四,代表单元在整个模型中是均匀地、规则地、周期性地分布的,而且每个代
表单元均是均匀和各向同性的(图1即为乳化沥青改性水泥砂浆细观力学模型)。
二、均匀化代表单元和边界约束
要分析乳化沥青改性水泥砂浆的有效弹性模量,只需从细观力学模型中取出一个代表单元进行研究。故选取其中一个边长为a正方形单元,其中心处有一个半径为圆和内径为、外径为同心圆环,其中中心圆形代表在单位面积内被乳化沥青包裹的未水化的水泥颗粒,阴影部分圆环为包裹未水化水泥颗粒的乳化沥青,正方形截面的其他部分代表已水化水泥生成的水泥砂浆。如图2(a)所示。根据代表单元的边界约束条件,即得到如图2(b)和图2(c)所示的约束形式。
三、选取模型参数
本文的数值计算,同样借助于通用有限元软件ANSYS进行,所取的试验参数为:未水化水泥颗粒的弹性模量,泊松比;水泥砂浆的弹性模量,泊松比;乳化沥青的弹性模量,泊松比;水灰比0.5;聚灰比5.5%。根据水灰比和聚灰比可以计算出代表单元的面积、未水化水泥颗粒的面积、乳化沥青的面积之间的比例关系。
在ANYSYS中仍然选用板单元PLANE2,在划分单元网格时,同样采用相同的单元尺寸,以利于后面的计算。
本文的计算是通过对代表单元施加一定值的初应变,计算得到对应的应力值,由于采用相同尺寸的单元网格,计算得到的每个单元的应力和应变的平均值就是代表单元的平均应力和平均应变,然后计算得到乳化沥青改性水泥砂浆的弹性模量和泊松比。
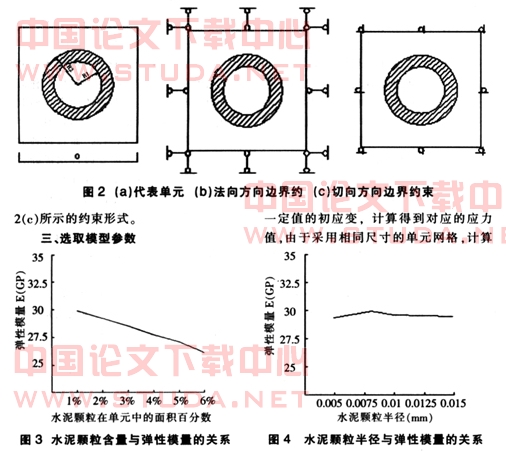
然后通过修改不同的条件参数,例如:调整水泥颗粒在代表单元中的百分含量、改变水泥颗粒的半径、通过调整聚灰比改变乳化沥青相在代表单元中的面积百分比以及变化初应变值等方式,研究各种因素对于水泥砂浆的弹性模量的影响情况。
五、主要结论
第一,随着未水化水泥颗粒在水泥砂浆中的含量的提高,水泥砂浆的弹性模量值呈明显的下降趋势,而且降幅达到10%,如图3所示。说明在实际运用中应该使乳化沥青包裹尽量多的未水化水泥颗粒,这样有利于降低水泥砂浆的弹性模量。
第二,如图4所示,尽管改变未水化颗粒的半径,但是对于弹性模量的影响不是十分显著,整个变化幅度不超过5%;证明乳化沥青包裹的水泥颗粒的半径对于弹性模量的影响可以忽略。
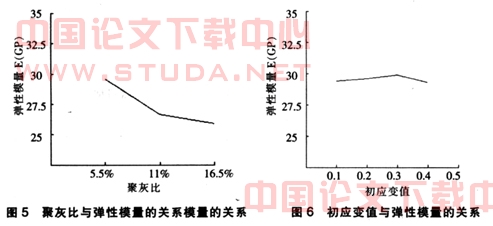
第三,如图5所示,随着聚灰比的增加,水泥砂浆的弹性模量呈现下降趋势,而且下降的幅度也比较大超过15%,可以证明随着聚灰比进一步增大,弹性模量还会继续下降。
第四,从图6可以发现,在对代表单元施加初应变值时,其引起的水泥砂浆的弹性模量的变化十分有限,基本控制在5%以内,所以初应变值对于水泥砂浆的弹性模量的影响可以忽略。
参考文献:
1、杨庆生.复合材料细观结构力学与设计[M].中国铁道出版社,2000.
2、苑学众.复合材料弹塑性有效性能研究[D].东北大学,2000.
3、Pribcigallo A,Lura P,van Breugel K.Early development of properties in a cement paste:A numerical and experimental study[J].Cem Concr Res ,2003(7).
4、咸淼.乳化沥青改性水泥基复合材料的研究[D].重庆交通大学,2005.
